517 编程具体数学初级班之组合数学
吴一岐
2020 年 5 月 19 日
1
前言
组合数学是计算机科学中的重要组成部分,在信息学竞赛中经常与数论,概率,动
态规划等需要计数的模型一起出现
并且,在各类复杂度分析,算法可行性分析,公式推导中,组合数学的内容也具有
重要的支撑作用,因此,锻炼扎实的组合数学基本功是非常必要的!
1
目录
目录
目录
1
前言
1
2
常见的一些符号表示的意义
4
3
基础知识
5
3.1
组合数的阶乘表示
5
3.2
递推公式
5
3.3
二项式定理
5
3.4
二项式定理的变形
6
3.5
组合数公式常见变形
6
3.6
隔板法
7
3.7
错位排列
7
3.8
圆排列
7
3.9
多重集合的排列
7
3.10
多重集合的组合
8
3.11
鸽巢原理
8
3.11.1
普通鸽巢原理
8
3.11.2
加强版鸽巢原理
8
4
康托展开
9
4.1
计算排列的排名
9
4.2
计算特定排名的排列
9
4.3
下一个排列
9
5
特殊的数列
10
5.1
第一类斯特林数
10
5.2
第二类斯特林数
10
5.3
卡特兰数
11
5.3.1
卡特兰数的其他形式
12
5.3.2
卡特兰数的一些应用 (信息学中初赛经常常用到)
12
6
放球问题汇总
13
6.1
球相同, 盒相同, 可以为空
13
6.2
球相同, 盒相同, 不能为空
13
2
517 编程内部讲义
目录
目录
6.3
球不同, 盒不同, 可以为空
14
6.4
球不同, 盒相同, 不能为空
14
6.5
球不同, 盒不同, 不能为空
14
6.6
球不同, 盒相同, 可以为空
14
6.7
球相同, 盒不同, 不能为空
14
6.8
球相同, 盒不同, 可以为空
14
7
组合数取模
14
7.1
第一阶段-普通阶乘逆元
15
7.2
第二阶段-卢卡斯定理
15
7.2.1
定理描述
15
7.2.2
定理证明
15
7.3
第三阶段-中国剩余定理合并
16
3
517 编程内部讲义
2
常见的一些符号表示的意义
2
常见的一些符号表示的意义
1.
a|b 表示 a 是 b 的约数
2.
⌊a
, 表示 a 除以 b 下取整
b⌋
∏
3.
pi 表示 p1,p2,...,pn 的乘积
i=1
∑
4.
ai 表示 a1,a2,...,an 的和
i=1
5.
a ≡ b (mod p) 表示 a 与 b 模 p 的结果是相同的
∑
6.
表示枚举 n 的所有因子 d
d|n
7.
f × g(x) 表示 f 函数与 g 函数的狄利克雷卷积
∫b
8.
a f(x)dx表示定积分
9.
f (x) = [x = 1] 表示 f (x) 只有在 x = 1 的时候才为 1,其他情况为
0
(n)
10.
与Cm
m
n 等价,都表示n个不同的小球取m个方案数
4
517 编程内部讲义
3
基础知识
3
基础知识
3.1
组合数的阶乘表示
(n)
n!
m =Cn =
m!(n − m)!
3.2
递推公式
(n)
(n−1)
(n − 1)
+
m =
m−1
m
预处理组合数
const int md = ; //模数
const int N = ; //数组大小
int c[N][N];
void init() {
c[0][0] = 1;
for (int i = 1; i < N; i++) {
c[i][i] = c[i][0] = 1;
for (int j = 1; j < i; j++) {
c[i][j] = c[i - 1][j] + c[i - 1][j - 1];
c[i][j] %= md;// 一般N范围较大的题目都需要取模
}
}
}
3.3
二项式定理
∑
(n)
k
(x + y)n =
k xn−ky
k=0
5
517 编程内部讲义
3.4
二项式定理的变形
3
基础知识
3.4
二项式定理的变形
∑
)
( n
1.
(x + y)n =
xn−kyk
n−k
k=0
∑
)
( n
2.
(x + y)n =
xkyn−k
n−k
k=0
∑
(n)
3.
(x + y)n =
xkyn−k
k
k=0
∑
(n)
∑
)
( n
4.
有一项为 1: (1 + x)n =
xk =
xk
k
n−k
k=0
k=0
(n)
(n)
(n)
5.
当 x = 2,y = 1 时即
20 +
21 + ... +
2n = 3n
0
1
n
(n)
(n)
(n)
(n)
6.
当 x = y = 1 时 (x − y)n =
−
+
− ... + (−1)n
= 0(n ≥
1)
0
1
2
n
(n)
(n)
(n)
(n)
7.
当 x = y = 1 时 (x + y)n =
+
+
+ ... +
=
2n(n ≥
1)
0
1
2
n
(n)
(n)
8.
+
+ ... = 2n−1
0
2
(n)
(n)
9.
+
+ ... = 2n−1
1
3
3.5
组合数公式常见变形
n, k 都是正整数,公式证明见视频
(n)
(n−1)
1. k
=n
k
k−1
(n)
(n)
(n)
2.
1
+2
+ ... + n
= n2n−1
1
2
n
(n−1)
(n−1)
(n−1)
3. n
+n
+ ... + n
= n2n−1
0
1
n−1
∑
(n)
4.
k2
= n(n + 1)2n−2
k
k=1
∑
(n)2
(2n)
5.
=
k
n
k=0
6
517 编程内部讲义
3.6
隔板法
3
基础知识
3.6
隔板法
n 个相同的小球放到 m 个不同的盒子里, 盒子不能为空,方案数为
(n−1)
m−1
上面这个也等价于 x1 + x2 + ... + xm = n 的正整数解的个数
n 个相同的小球放到 m 个不同的盒子里, 盒子可以为空, 可以先给每个盒子放一
个球, 问题等价于将 n+m 个相同的小球放入 m 个不同的盒子里, 不为空
(m + n − 1)
m−1
3.7
错位排列
每个数都不在自己位置的排列叫做错位排列,假设排列为 f1,f2...fn, 错位排列满
足对于所有的 1 ≤ i ≤ n, fi! = i
错排的递推公式
f [1] = 0, f [2] = 1
f [i] = (i − 1) ∗ (f [i − 2] + f [i − 1])(i > 3)
证明:假设将 i 放到 1 到 i − 1 的某个位置 j, 假设 j 这个数放到 i 位置, 那么方
案数就是剩下的 i − 2 个数进行错排, 假如 j 这个数不放在 i 的位置上, 那么就是 i − 1
个数进行错排, 注意这里思维的巧妙转换,i 位置相当于 j 的一个新的限制位置了
3.8
圆排列
对于每种排列, 循环移动一圈, 都算同一种排列, 相当于将总的排列分成了若干组,
每组的本质是相同的, 而且每组里面有 n 个排列, 那么本质不同的圆排列就有n!
n 种
3.9
多重集合的排列
设 S 是有 k 种不同类型对象的多重集合, 每一个元素都有无线重复数, 那么,S 的
r 排列的数量是 kr
设 S 是多重集合, 它有 k 种不同类型的对象, 且每一种类型的有限重复数分别为
n1,n2,...,nk 设 S 的大小为 n = n1 + n2 + ... + nk. 则 S 的排列数目等于
n!
n1!n2!...nk!
7
517 编程内部讲义
3.10
多重集合的组合
3
基础知识
证明: 相当于先选出 n1 个位置, 再选出 n2 个位置...
)
( n )(n − n1)(n − n1 − n2
(n − n1 − n2 − ... − nk−1)
n1
n2
n3
nk
化简这个式子就可以证明了
3.10
多重集合的组合
设 S 是有 n 种类型的对象的多重集合, 每种元素均有无限的重复数, 那么 S 的 k
组合的个数等于
(n + k − 1)
(n + k − 1)
=
k
n−1
问题等价于选 k 次球, 每次都可以选 n 种球的方案数, 选球不分先后
等价于 k 个相同的球放到 n 个不同的盒子里, 盒子可以为空
3.11
鸽巢原理
3.11.1
普通鸽巢原理
如果要把 n + 1 个物体放进 n 个盒子,那么至少有一个盒子包含两个或更多的物
体
比如,在 13 个人中一定存在两个人生日是同一月份,n 对新婚夫妇,选择 n + 1
人就一定会包含一对新婚夫妇。
3.11.2
加强版鸽巢原理
设 q1,q2,...,qn 是正整数,如果将 q1 + q2 + ... + qn − n + 1 个物体放入 n 个盒子
内,那么或者第一个盒子至少含有 q1 个物体,或者第二个盒子至少含有 q2 个物体,...,
或者第 n 个盒子至少含有 qn 个物体
证明:采用反证法,假设第 i 个盒子含有少于 qi 个物体,那么所有盒子中的物体
总数不超过
(q1 − 1) + (q2 − 1) + ... + (qn − 1) = q1 + q2 + ... + qn − n
8
517 编程内部讲义
4
康托展开
4
康托展开
4.1
计算排列的排名
给你一个排列, 计算这个排列之前的排列总数公式为
X = a1(n − 1)! + a2(n − 2)! + ... + an0!
ai 是从左往右数的第 i 个数右边小于它的数的个数
比如 [2, 3, 4, 1], 那么 a1 = 1, a2 = 1, a3 = 1, a4 = 0
因此 X = 1 ∗ 3! + 1 ∗ 2! + 1 ∗ 1! + 0 = 9,表示这个排列前面一共有 9 个排列,这
个排列是第 10 个排列
4.2
计算特定排名的排列
这个方法也经常叫康托展开的逆展开,也就是告诉你一个排列的排名, 让你复原这
个排列
比如让你求五个数的 107 个排列是谁, 假设第一个是 12345
假设排列的编号从 0 开始, 那么我们就是求编号为 106 的排列
利用康托展开的公式,从高到低确定每一位
106
= 4 , 余 10, 说明第一位右边有 4 个比它小, 所以最高位为 5
4!
10
= 1, 余 4, 说明第二位右边有 1 个比它小, 所以当前位为 2
3!
4
= 2, 余 0, 说明第三位右边有 2 个比它小, 所以当前位为 4
2!
0
= 0, 余 0,说明第四位右边没有数比它小,所以当前位为 1
1!
最后一位为 3
可以得到最终排列为 [5, 2, 4, 1, 3]
思想类似于进制转换
4.3
下一个排列
这里顺便提一下如何比较简单的寻找某个排列的下一个排列,对于一个排列 p1, p2, ..., pn,
我们从后往前扫描,找到第一个 pi < pi+1 的地方,然后从后往前找到第一个 pj < pi
将 pi 与 pj 交换,然后将 i 位置以后的所有元素颠倒过来
比如 [1, 2, 5, 7, 6, 4, 3] , 找到第一对 pi < pi+1 是 (5, 7), 从后往前找到一个数 6 比 5
要大,交换后得到 [1, 2, 6, 7, 5, 4, 3],然后将 [7, 5, 4, 3] 反转可得 [1, 2, 6, 7, 3, 4, 5]
9
517 编程内部讲义
5
特殊的数列
5
特殊的数列
5.1
第一类斯特林数
将 n 个不同物体排成 k 个非空环的方案数
dp[n][k] = (n − 1)dp[n − 1][k] + dp[n − 1][k − 1]
要么自己成一个环, 要么凑到之前的某个环里, 凑到之前的环里一共有 n −
1
种空
位可以插入
第一类斯特林数
void init(int n) {
dp[0][0]=dp[1][1]=1;
for(int i=2;i<=n;i++){
for(int j=1;j<=i;j++){
dp[i][j]=dp[i-1][j-1]+(i-1)*dp[i-1][j];
dp[i][j]%=MOD;
}
}
}
5.2
第二类斯特林数
将 n 个不同物体分成 k 个非空集合的方案数
相当于将 n 个不同的小球, 放到 k 个相同的盒子里, 不能为空
dp[n][k] = k ∗ dp[n − 1][k] + dp[n − 1][k − 1]
即, 当前这个球要么放到之前的盒子里, 要么新开一个盒子
10
517 编程内部讲义
5.3
卡特兰数
5
特殊的数列
第一类斯特林数
void init(int n){
for(int i=0;i<=n;i++){
dp[i][i]=dp[i][1]=1;
for(int j=2;j<i;j++){
dp[i][j]=(dp[i-1][j-1]+1LL*j*dp[i-1][j]%MOD)%MOD;
}
}
}
5.3
卡特兰数
11
517 编程内部讲义
5.3
卡特兰数
5
特殊的数列
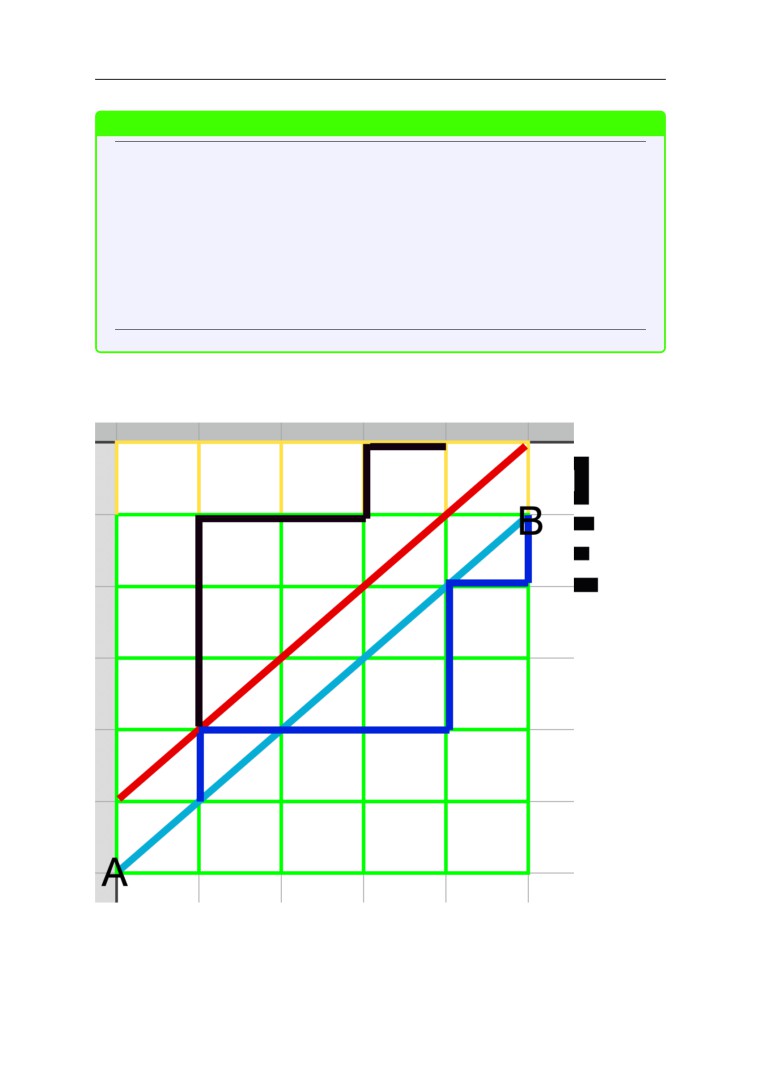
假如有一个 n ∗ n 的网格,从左下角的 A 点走到右上角的 B 点, 始终不超过对角
线的走法有多少种
观察上图可得, 任何一条非法路径一定存在一个中间点在对角线上方, 也就是会碰
到红色的那条线, 假设第一个碰到的是 P
我们从 P 点开始, 将之后的那部分蓝色的线, 按照对角线上方的斜线做对称, 最终
到达的点为 (n − 1, n + 1)
我们会发现任何一种非法方案都可以对称成 (0, 0) 到 (n − 1, n + 1) 的一条路径, 他
(2n)
(2n
)
们之间存在一一映射关系, 所以总方案数是
−
n
n+1
化简上面这个式子
)
(
)
(2n
2n
Catalan(n) =
−
n
n+1
(2n)!
= (2n)!
−
n!n!
(n+1)!(n−1)!
=1
− (2n)!
n+1 ((2nn!!
!
n!(n−1)! )
=1
−(2n)!∗n
n+1 ((2nn!!
!
n!n!
=1(2n)!(n+1)−(2n)!∗n
n+1
n!n!
=1(2n)!
n+1 n!n!
(2n)
=1
n+1
n
5.3.1
卡特兰数的其他形式
∑
(n)2
1
C(n) =
n+1
i
i=0
∑
C(n + 1) = C(i)C(n − i), C(0) = 1
i=0
C(n + 1) =2(2n+1)C(n), C(0) = 1
n+2
5.3.2
卡特兰数的一些应用 (信息学中初赛经常常用到)
1. n 对括号的合法匹配的方案数
2. n 个节点二叉树的形态数
3. n+1 个叶子 (n 个非叶节点) 的满二叉树(每个节点都有两个儿子或者没有儿子)
的形态数, 走到左儿子 +1, 走到右儿子-1, 类似于括号匹配.2 , 3 两种情况其实是
一回事
4. n 个数入栈后出栈的排列总数
12
517 编程内部讲义
6
放球问题汇总
5. 对凸 n+2 边形进行不同的三角形分割的方案数, 分割点不能交叉, 可以在端点处
相交
选择一条基础边, 中间的三角形将整个多边形劈开两半, 变成了两个子问题, 就可
以用卡特兰数的其他形式中的第二种形式来做了.
6
放球问题汇总
n 个球放到 m 个盒子里
6.1
球相同, 盒相同, 可以为空
等价于整数拆分问题,比如将 7 拆分成小于等于 3 个数的方案有 [1,1,5], [1,2,4],
[1,6] 等,注意,由于盒子是相同的,所以 [1,1,5] 和 [1,5,1] 是同一种方案
我们可以用 dp[i][j] 表示 i 个球放到 j 个盒子里的方案数
转移方程为 dp[i][j] = dp[i][j − 1] + dp[i − j][j]
两种转移分别表示
1: 放入小球后,球最少的盒子为空,相当于将 i 个小球放入 j−1 个盒子里,dp[i][j−
1]
2: 放入小球后,球最少的盒子不为空,说明每个盒子里面都有球,可以从 dp[i−j][j]
转移过来
关于整数拆分的延伸阅读
6.2
球相同, 盒相同, 不能为空
不能为空就可以利用上面整数拆分的结果,dp[i][j] - dp[i][j-1]
13
517 编程内部讲义
6.3
球不同, 盒不同, 可以为空
7
组合数取模
6.3
球不同, 盒不同, 可以为空
每个球都有 m 种不同的选择
答案为 nm
6.4
球不同, 盒相同, 不能为空
dp[i][j], 将 i 个球放入 j 个盒子里的方案数
当前这个球一种选择是放入之前的某个盒子,虽然盒子是相同的,但是因为球是
不同的导致当前这个球放入这 j 个盒子的某一个有 j 种选择
另一种选择是不放入之前的盒子,放入一个新盒子
dp[i][j] = j ∗ dp[i − 1][j] + dp[i − 1][j − 1]
所以这个本质上就是第二类斯特林数,等价于将 i 个不同的小球分成了 j 个非空
集合的方案数
6.5
球不同, 盒不同, 不能为空
先假设盒子都是相同的,问题就转换成了前一个问题,最后因为盒子不同,所以
任意一种排列都是不同的。
答案等于 dp[n][m] ∗ m!
6.6
球不同, 盒相同, 可以为空
还是跟第二类斯特林数一样,可以为空就相当于枚举一下最终用了几个盒子求和
即可
6.7
球相同, 盒不同, 不能为空
(n−1)
经典的隔板法,
m−1
6.8
球相同, 盒不同, 可以为空
(m+n−1)
n−1
7
组合数取模
(n)
求
(mod p)
m
14
517 编程内部讲义
7.1
第一阶段-普通阶乘逆元
7
组合数取模
7.1
第一阶段-普通阶乘逆元
数据范围:n, m ≤ 1e6
p 是质数,直接利用阶乘逆元,费马小定理搞定
7.2
第二阶段-卢卡斯定理
数据范围:n, m ≤ 1e18, p 是质数 p ≤ 1e6
7.2.1
定理描述
首先,我们将 n, m 写成 p 进制数的形式
n = (a0a1...ak)p
m = (b0b1...bk)p
那么
∏
(ai)
(mod p)
m ≡
bi
i=0
也可以用递归的形式来表示这个式子
(n)
( n%p)( n/p)
(mod p)
m ≡
m%p m/p
我们发现如果上面的这个式子成立的话,我们就可以一直递归到 n < p,m < p 的
时候再进行计算
7.2.2
定理证明
首先介绍一个引理:
(a + b)p ≡ ap + bp
(mod p)
证明:根据费马小定理 (a + b)p ≡ a + b ≡ ap + bp (mod p)
因此
(1 + x)p ≡ 1 + xp
(mod p)
假设 n%p = b
(1 + x)n ≡ (1 + x)⌊p ⌋p(1 + x)b
(mod p)
15
517
编程内部讲义
7.3
第三阶段-中国剩余定理合并
7
组合数取模
≡ (1 + xp)⌊p ⌋(1 + x)b
(mod p)
二项式展开后变成如下式子
∑(⌊n
∑(b)
p⌋)
xpi
i
j xj
i=0
j=0
注意这个式子与 (1 + x)n 的展开是等价的, 我们观察对于某一个 xm 的系数,在
(n)
(1 + x)n 里面是
而在上面这个式子中 xm 被分成了两个部分,假设 m = i ∗ p + j.
m
(j < p), 所以有
(n)
(⌊n
p⌋)(b)
(m = i ∗ p + j, j < p)
m =
i
j
i=⌊m
p ⌋,b=n%p,j=m%p,所以有
(n)
(⌊n
p⌋)(n%p)
m =
⌊m
m%p
p ⌋
复杂度为 O(logn
p)
卢卡斯定理
int binom(int n, int m) {
if (n < m) return 0;
return 1LL * fac[n] * inv(fac[m]) % md * inv(fac[n - m]) %
md;
}
int lucas(int n, int m) {
if (m == 0) return 1;
return 1LL * lucas(n / md, m / md) * binom(n % md, m % md)
% md;
}
7.3
第三阶段-中国剩余定理合并
数据范围:n, m ≤ 1018, p ≤ 106 (p 不一定是质数)
我们可以先将 p 进行质因数分解,然后求组合数对于每个 pai
i 取模的结果,最后
使用中国剩余定理进行答案的合并, 于是,现在我们需要求
16
517 编程内部讲义
7.3
第三阶段-中国剩余定理合并
7
组合数取模
(n)
ai
(mod p
)
i
m
将组合数写成阶乘的形式
n!
m!(n − m)!
由于分母可能包含质因子 pi, 于是不能直接求分母对 pai
的逆元,可以考虑将
i
分子分母中包含的 pi 全部提取出去,最后再乘回去所以现在最关键的就是要求n!
px
i
(mod pai), 即算出分子和分母的阶乘去除 pi 因子后对 pai
取模,去掉之后就可以正
i
i
常使用逆元
接下来以 19! (mod 32) 为例
19! = 1 ∗ 2 ∗ 3... ∗ 17 ∗ 18 ∗ 19
= 1 ∗ 2 ∗ 4 ∗ 5 ∗ 7 ∗ 8 ∗ 10 ∗ 11 ∗ 13 ∗ 14 ∗ 16 ∗ 17 ∗ 19 ∗ (3 ∗ 6 ∗ 9 ∗ 12 ∗ 15 ∗ 18)
= (1 ∗ 2 ∗ 4 ∗ 5 ∗ 7 ∗ 8) ∗ (10 ∗ 11 ∗ 13 ∗ 14 ∗ 16 ∗ 17) ∗ 19 ∗ 36 ∗ (1 ∗ 2 ∗ 3 ∗ 4 ∗ 5 ∗ 6)
36 ∗ (1 ∗ 2 ∗ 3 ∗ 4 ∗ 5 ∗ 6) 相当于先提取出所有 pi 的倍数,然后, 每个数再提取出一
个 pi, 最后变成 n/pi 的阶乘,这个可以递归求解
(1 ∗ 2 ∗ 4 ∗ 5 ∗ 7 ∗ 8) 与 (10 ∗ 11 ∗ 13 ∗ 14 ∗ 16 ∗ 17) 模 pai
i 是相等的,说明有循环节,
所以我们只需算出一个括号内的然后快速幂计算所有循环
最后剩下一部分零头的数量一定小于 pai, 可以暴力计算
i
17
517 编程内部讲义