题目大意

给出一棵以1为根的有根树,每个非叶子节点都有一条到其儿子节点的有向边.每个非根节点都有一条到根的返祖边.有$q$个询问,每次修改一条边的权值或者查询树上两点间的最短路

树上距离

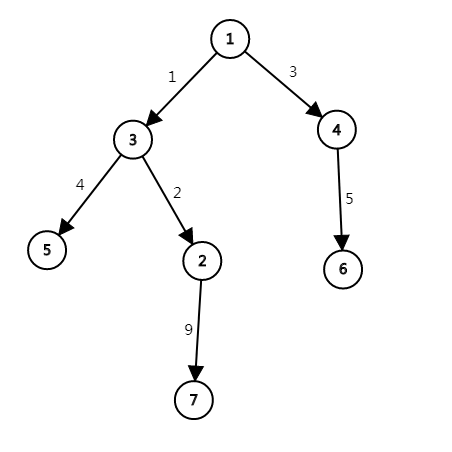
按照题目大意建出一棵树
因为所有的树边都是有向边,所以树上的距离有如下性质
当且仅当u为v的祖先时u->v才有树上的路径
记树上距离(u,v)为$dis(u,v)$

中转站:根

每一个点都有一条到根的返祖边,设$u$的返祖边长度为$len(u)$
因为根是所有点的祖先,以根为中转站,$u\Rightarrow v$的路径可以改写成$u\Rightarrow 1 \Rightarrow v$
此时距离为$len(u)+dis(1,u)$
可以证明,中间只会跳到根节点一次.
否则距离则为$len(u)+dis(1,p)+len(p)+dis(1,u)<len(u)+dis(1,u)$

中转站:子树

$u$是其子树所有点的祖先,故$u$可以到达其子树中的点$p$.
故此时$u\Rightarrow v$的距离为$dis(u,p)+len(p)+dis(1,v)$

最短路

若$u$为$v$的祖先,则答案很明了
就是$dis(u,v)$,因为$dis(u,v)<=dis(1,v)<len(p)+dis(1,v)(p在u的子树内)$
否则$u\Rightarrow v$的距离为
$res=min (dis(u,p)+len(p)+dis(1,v))$
$res=min (dis(1,p)+len(p))-dis(1,u)+dis(1,v)$
$dis(1,u)$和$dis(1,v)$在查询的时候是固定的
故方向很明了了,只需要求$u$子树内$min(dis(1,p)+len(p))$
由于是区间/单点更新权值,而区间查询的是最值,故用线段树维护比较方便

维护&查询

线段树需要的功能

1.在修改树边的时候把整个子树的权值加上更改的权值
2.在修改返祖边的时候把一个点的权值加上更改的权值
3.区间查询整个区间的$dis(1,p)+len(p)$
4.单点查询某个点$p$的$dis(1,p)+len(p)-len(p)$

解决的是子树的问题,故用dfs序维护即可,不需树链剖分
其次,判断$u$和$v$是否为祖先关系的时候也可以用dfs序
若$v$的dfs序在$u$的子树的dfs序区间内,则$u$为$v$的祖先
即$L[u]<L[v]\ and\ L[v]<=R[u]$
由于这道题比较阴间,可能出现$u==v$的情况
所以这个判断是$L[u]<=L[v]\ and\ L[v]<=R[u]$

代码

把自己考场代码优化了一下,因为原本求$dis(1,u)$的时候用的是树状数组(因为感觉写起来比线段树方便)

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+5,M=N<<1;
typedef long long LL;
int n,Q,fa[N],dep[N],len[N],L[N],R[N],Re[N];
int nxt[N],to[N],head[N],val[N],tot,U[M],V[M],W[M];
LL dis[N];
void Add(int u,int v,int w)
{
    nxt[++tot]=head[u];
    to[head[u]=tot]=v;
    val[tot]=w;
}
void dfs(int u,int f)
{
    dep[Re[L[u]=++tot]=u]=dep[fa[u]=f]+1;
    for(int i=head[u];i;i=nxt[i])
    {
        int v=to[i];
        if(v==f)continue;
        dis[v]=dis[u]+val[i];
        dfs(v,u);
    }R[u]=tot;
}
struct Seg
{
    LL Sum[N<<2],lz[N<<2];
    #define ls p<<1
    #define rs p<<1|1
    #define Lson L,mid,ls
    #define Rson mid+1,R,rs
    #define LRP int L=1,int R=n,int p=1
    //个人打线段树常用的define
    void Chg(int p,int x)//修改
    {
        Sum[p]+=x,lz[p]+=x;
    }
    void Down(int p)//延迟更新
    {
        LL &t=lz[p];
        if(!t)return ;
        Chg(ls,t);
        Chg(rs,t);
        t=0;
    }
    void Updata(int l,int r,int x,LRP)//区间更新
    {
        if(L==l&&r==R)return Chg(p,x);
        Down(p);int mid=L+R>>1;
        if(r<=mid)Updata(l,r,x,Lson);
        else if(l>mid)Updata(l,r,x,Rson);
        else Updata(l,mid,x,Lson),Updata(mid+1,r,x,Rson);
        Sum[p]=min(Sum[ls],Sum[rs]);
    }
    void Updata_(int x,int y,LRP)//单点更新
    {
        if(L==R)return Sum[p]+=y,void();
        Down(p);int mid=L+R>>1;
        if(x<=mid)Updata_(x,y,Lson);
        else Updata_(x,y,Rson);
        Sum[p]=min(Sum[ls],Sum[rs]);
    }
    void Build(LRP)//建线段树
    {
        if(L==R)
        {
            int u=Re[L];
            Sum[p]=dis[u]+len[u];
            return ;
        }
        int mid=L+R>>1;
        Build(Lson),Build(Rson);
        Sum[p]=min(Sum[ls],Sum[rs]);
    }
    LL Query(int l,int r,LRP)//区间查询
    {
        if(L==l&&r==R)return Sum[p];
        Down(p);int mid=L+R>>1;
        if(r<=mid)return Query(l,r,Lson);
        if(l>mid)return Query(l,r,Rson);
        return min(Query(l,mid,Lson),Query(mid+1,r,Rson));
    }
    LL Query_(int x,LRP)//单点查询
    {
        if(L==R)return Sum[p]-len[Re[L]];
        Down(p);int mid=L+R>>1;
        if(x<=mid)return Query_(x,Lson);
        return Query_(x,Rson);
    }
}T;
int main()
{
    cin>>n>>Q;
    for(int i=1;i<n;++i)
        scanf("%d%d%d",&U[i],&V[i],&W[i]),
        Add(U[i],V[i],W[i]),swap(U[i],V[i]);
    dfs(1,tot=0);
    for(int i=n;i<=n+n-2;++i)
        scanf("%d%d%d",&U[i],&V[i],&W[i]),len[U[i]]=W[i];
    T.Build();
    for(int op,u,v;Q--;)
    {
        scanf("%d%d%d",&op,&u,&v);
        if(op==1)
        {
            int p=U[u];
            if(u<n)T.Updata(L[p],R[p],v-W[u]);
            else T.Updata_(L[p],v-W[u]),len[p]=v;
            W[u]=v;
        }
        else
            if(L[u]<=L[v]&&L[v]<=R[u])//v是u的后代
                printf("%lld\n",T.Query_(L[v])-T.Query_(L[u]));
            else//否则求区间最小值
                printf("%lld\n",T.Query(L[u],R[u])-T.Query_(L[u])+T.Query_(L[v]));
    }
}