dfs树-tarjan系列点双,边双,强联通
dfs树与随机数
Dijkstra (heap)
Floyd
⽆向图最小环
bellman-ford/spfa
差分约束
topological sorting
图的绝对中⼼
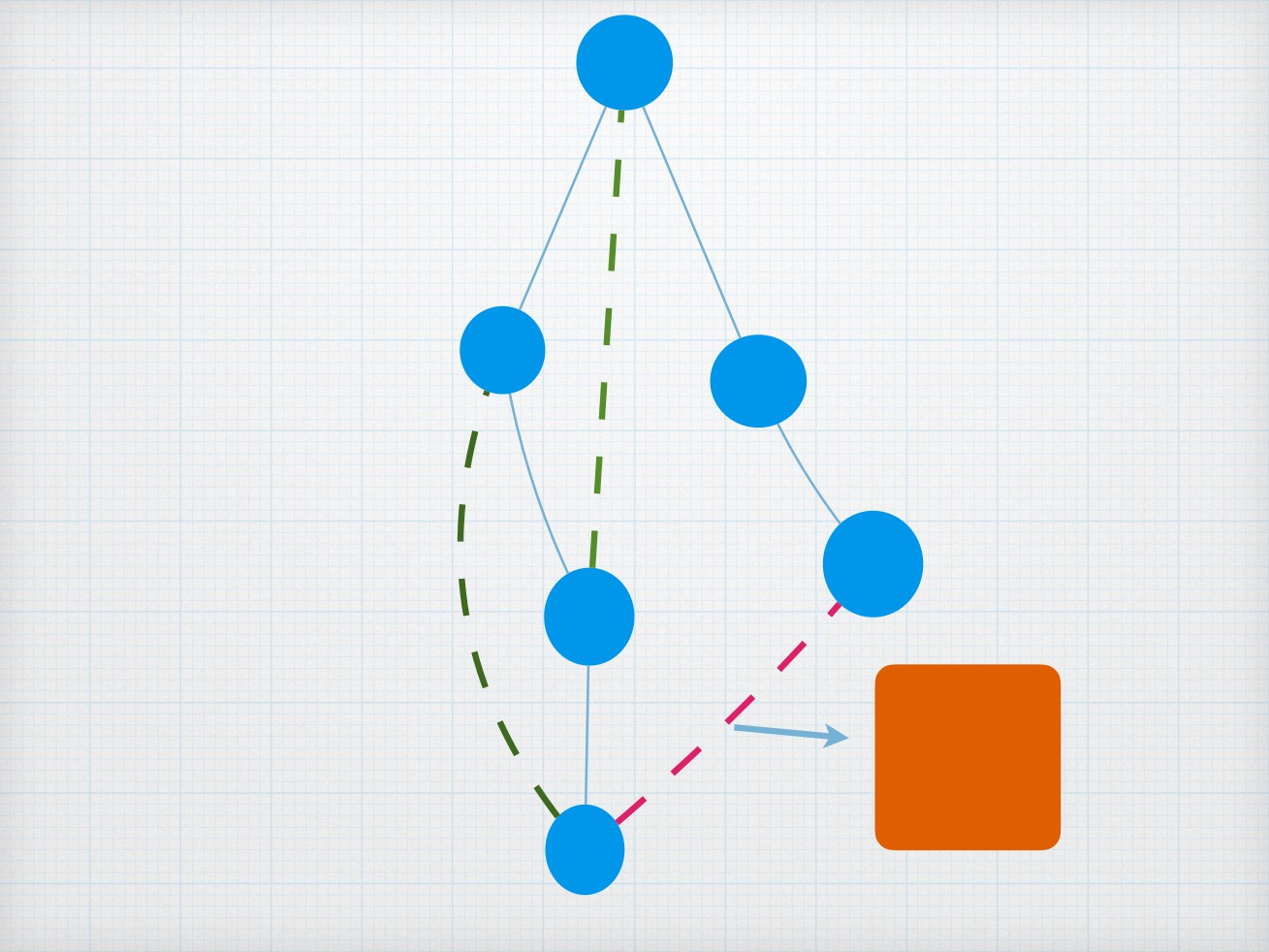
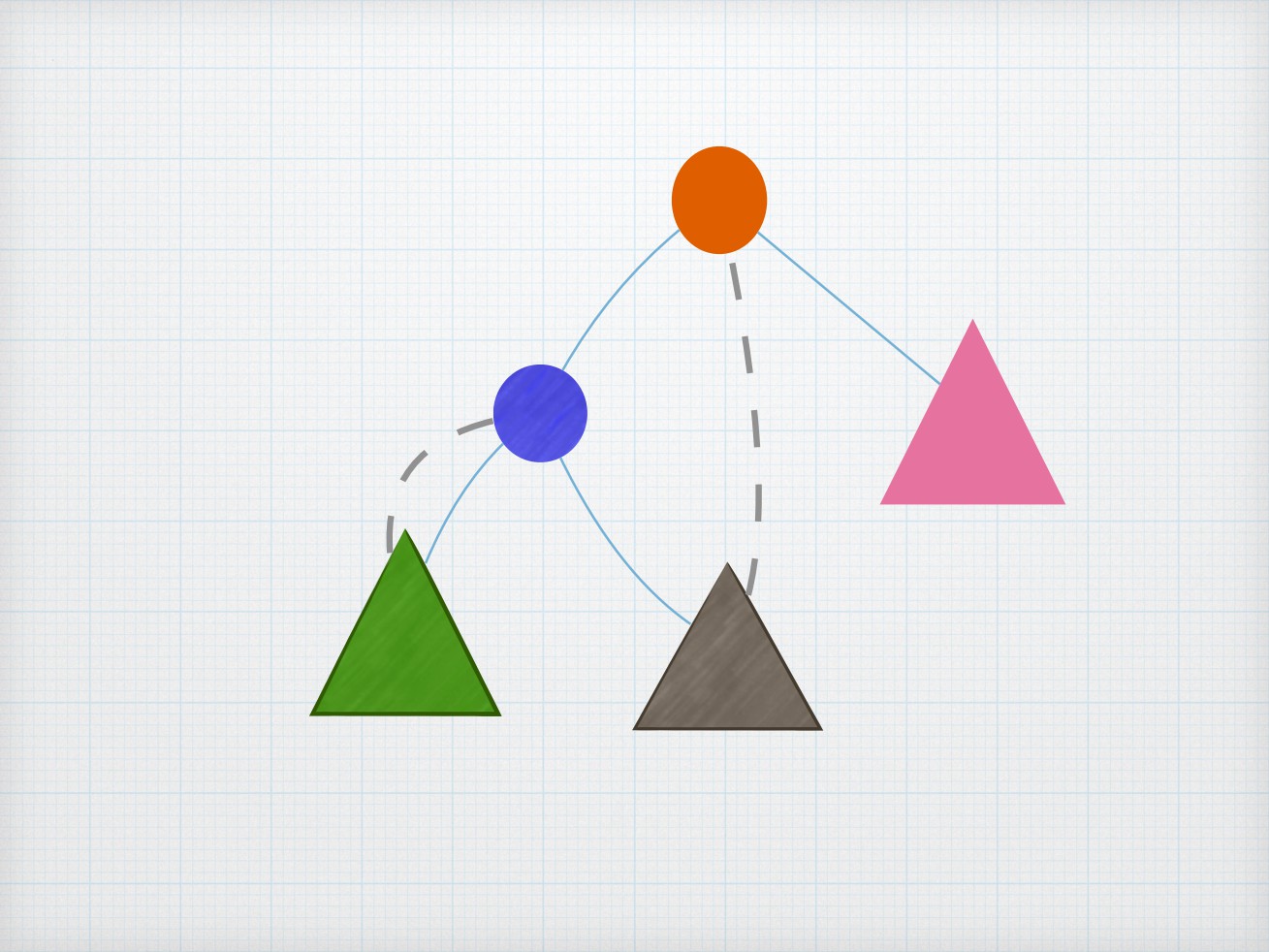
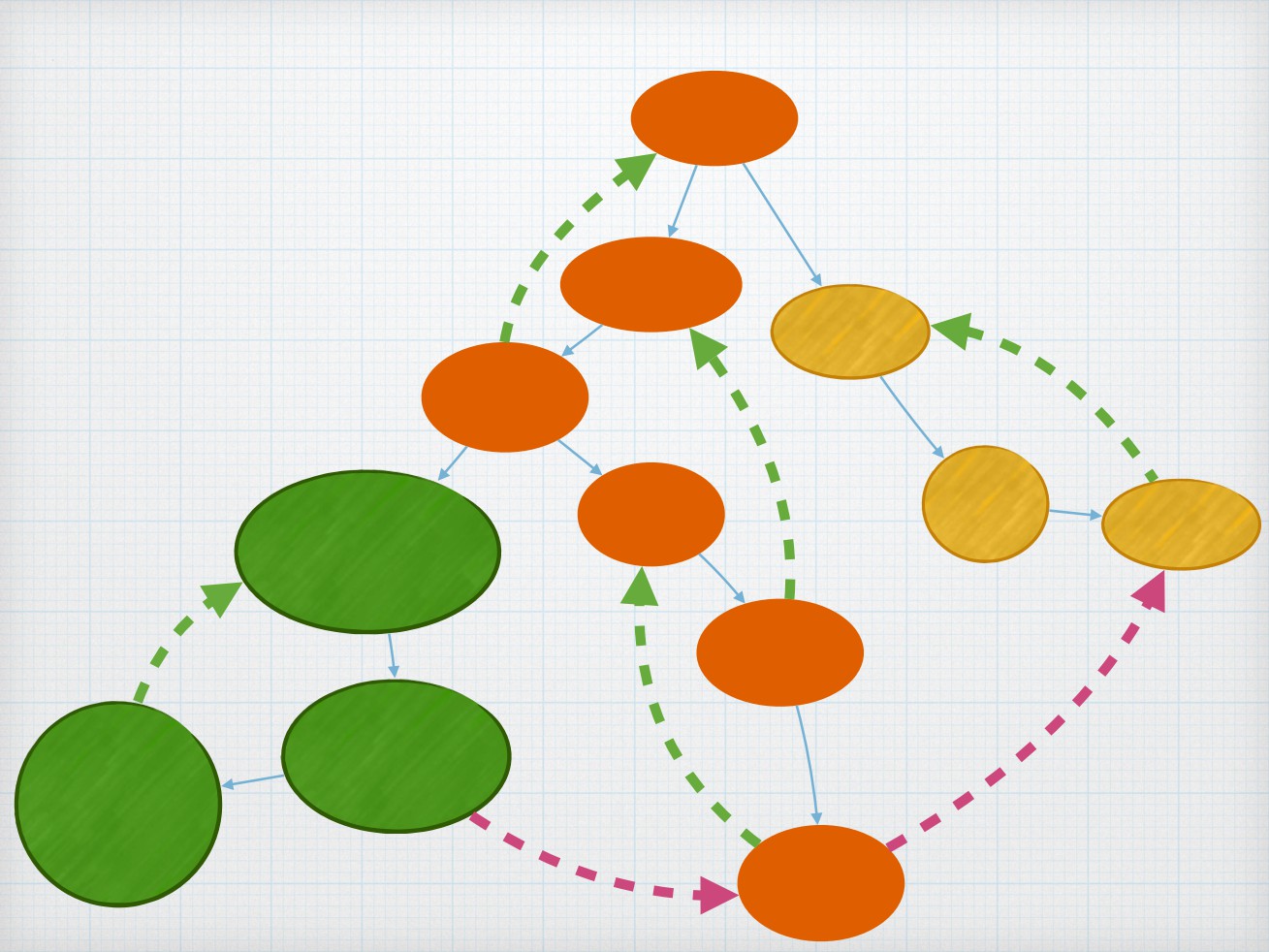
dfs树
对⼀副图进⾏dfs后按照dfs的顺序形成的⼀棵⽣成
树
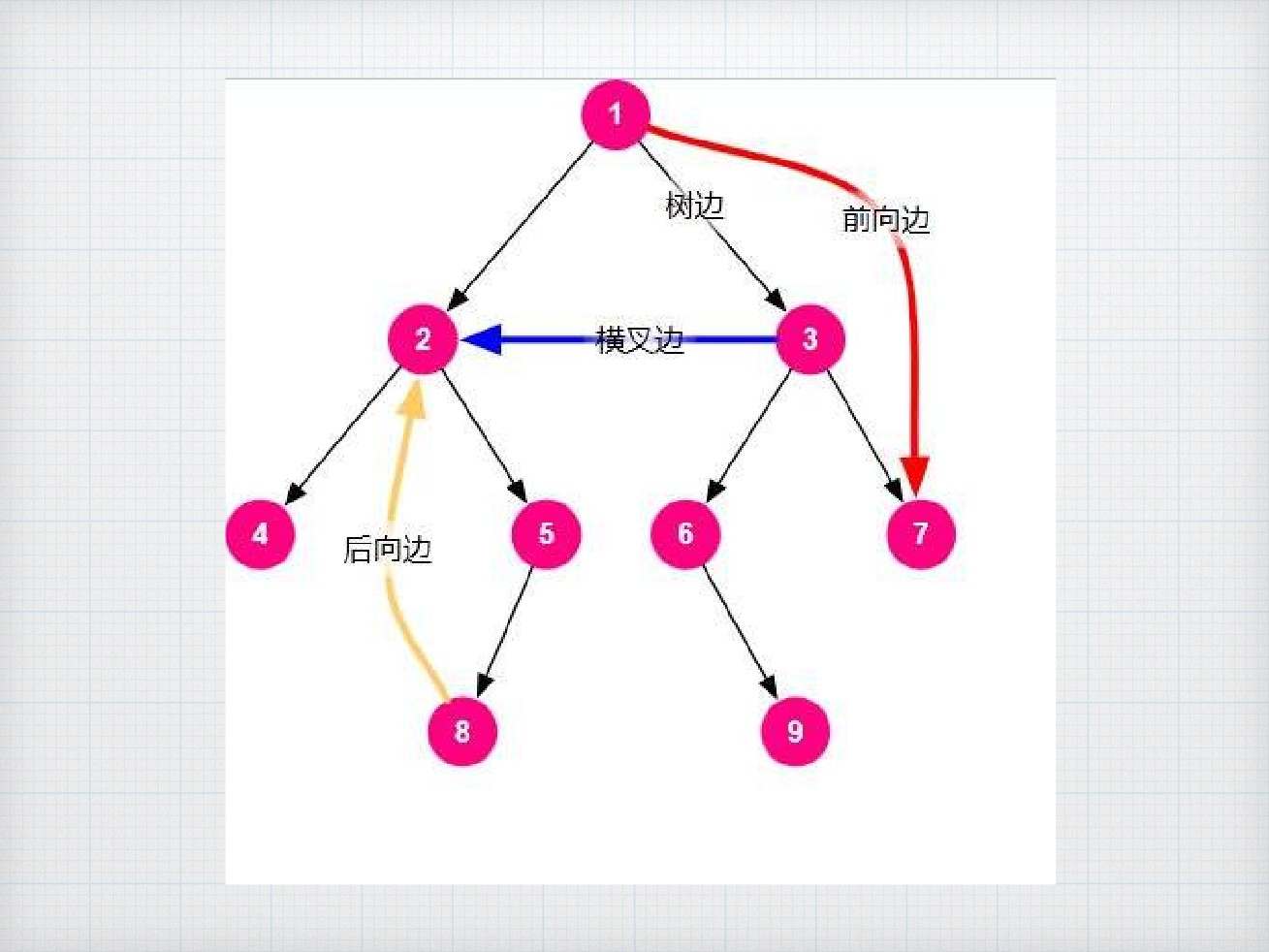
图中的边可以分为树边与非树边
⽆向图中,非树边只会以返祖边(后向边)的形式
存在
有向图中,非树边还会以前向边与横叉边的形式存
在
割点
去掉割点后,图会不连通
树的非叶节点都是割点
割点的两种情况
1:根节点在dfs树中有两个或以上的
⼉⼦,根节点为割点
2:非根节点u⾄少有⼀个⼦树没有返
祖边可以跨过u
割边
去掉割边后图就不连通,也称为桥
⼀条边是割边当且仅当⼦树内返祖边都
⽆法跨过这条边
将所有的割边去掉后,整个图会分成若
⼲个双联通分量(双联通⼦图),每⼀
个联通块内去掉⼀条边还是连通
点双与边双具体求法
每个节点维护两个信息
1:第⼀次访问到的时间戳dfn
2:当前节点以及⼦树内部通过返祖边最早能访问到的时间戳low
如果low[from] == dfn[from]说明from上面的那条边就是割边
low[to] >= dfn[from]说明to⼦树⽆法返回到from上面,from为割点
dfs的时候用⼀个栈保存搜到的点,回溯的时候⼀旦发现low[from] ==
dfn[from]就将栈中from⼦树内的点都退出,并标记成同⼀个连通分量
求边双也可以使用树上差分,每条返祖边覆盖⼀段路径,割边被返祖边覆
盖的次数为0
S
失去信仰退栈
A
I
low = dfn
B
J
F
C
K
D
G
E
信仰坚定
H
环环相扣
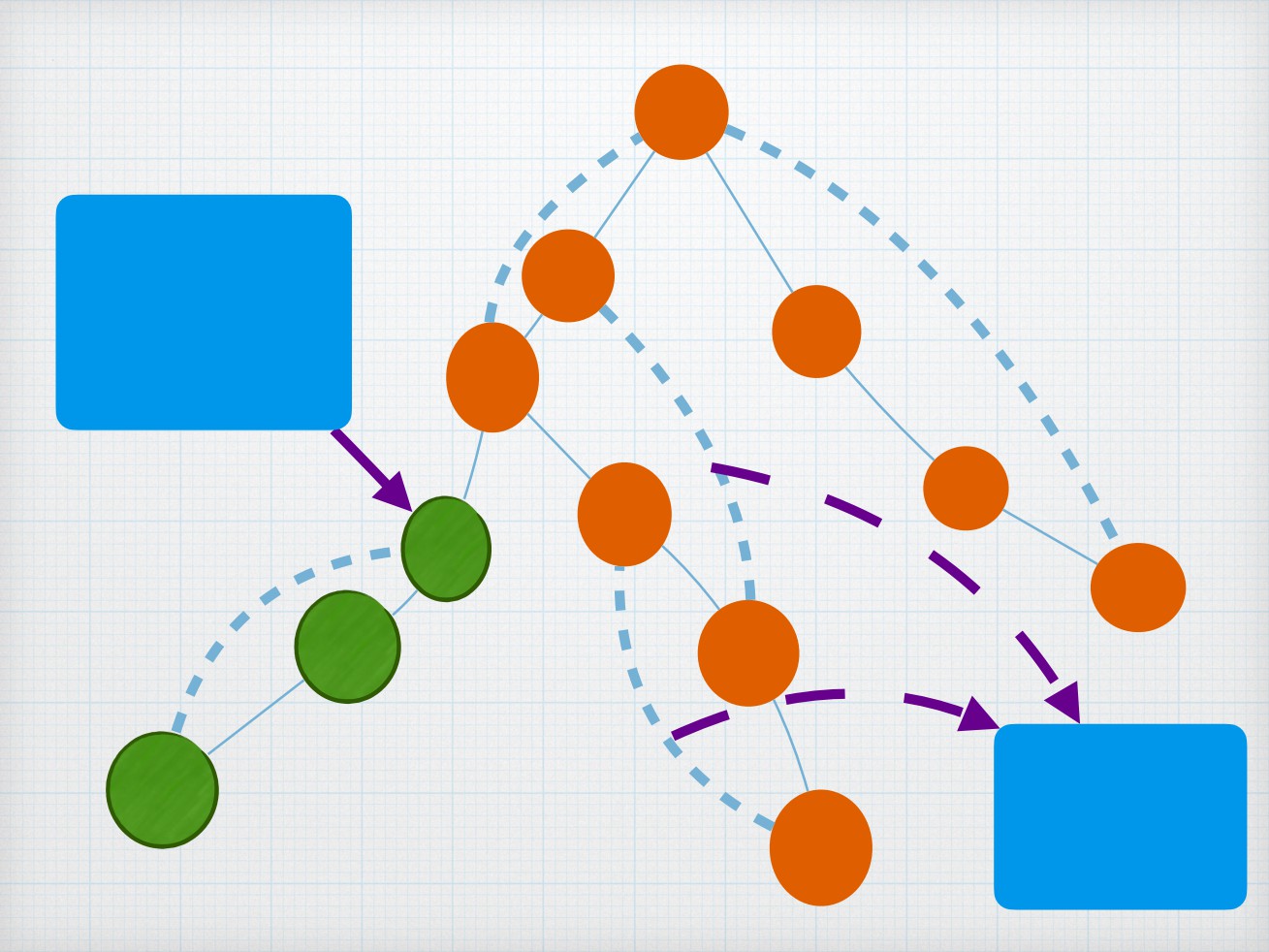
强连通
强连通是针对有向图⽽⾔的
强连通分量(Strong Connected components) 内部两两
之间都有⼀条通路(s->t, t->s)
强连通分量(极⼤强连通⼦图)缩点之后会构成⼀
副有向⽆环图(DAG)
四种边:树边,返祖边(后向边),前向边,横插
边
强连通分量求法
基本类似于边双的求法,用⼀个栈保存搜到的点,更新low值的时
候,如果相邻的点已经访问过,这个点⼀定要在栈里面,不在栈里面
的已经访问过的点是已经与别的点构成了强连通分量的点,比如H->K
的边
性质1: 当low[x]==dfn[x]的时候执⾏出栈操作,将x能搜到的点都退
栈,他们构成了⼀个强连通分量,它们通过返祖边或者横叉边能直接
或者间接的到达x
性质2:但是每个强连通分量都会在最⾼点求出来
性质3:如果low值是通过横叉边更新的,说明通过横叉边可以到LCA再
到自⼰,形成⼀个环
S1_1
A5_1
I2_2
B6_1
J3_2
F7_5
K4_2
C_10_10
G8_5
D_11_10
E_12_10
H9_7
dfs树与随机数
给出⼀个⽆向图,每次询问删掉给定
的k条边后图是否连通
n<=100000,m<=500000,q<=50000,k<=15
构造dfs树,非树边rand⼀个值
树边的值等于所有覆盖它的非树边的
值的xor
问题等价于是否存在⼀个⼦集的xor和
为0
同样的思路可以用来求割边的数量
Dijkstra
类似于prim,将节点分成两类,已确
定最短距离节点与未确定点。每次从
未确定点集中选取距离值最小的⼀个
点加⼊到最短路点集中,因为这个点
的最短路径不可能再被更新了,然后
用这个点的最短路径去更新邻接点的
最短路径
djikstra+heap
用⼀个堆维护距离的最小值,每次从堆中取
出⼀个最小的值,如果这个值⼤于当前真实
的距离,就不要,因为有可能被放⼊堆之
后,又被别的点更新了最短路,当确定是最
短路后,就拿这个点的最短路去更新相邻
点,把它们的距离值放⼊堆中,因此⼀个点
会⼊堆多次,⼊堆总次数为边的数量,复杂
度应该为mlogm
floyd
经典的三个循环
考虑某⼀条最短路的形成过程,当路径上的点被⼀个
个考虑进来的时候,会形成⼀段段区间,每⼀段区间
内部的两两之间的最短路都已经求出,每加⼊⼀个点
会连通两个相邻的区间。左区间到右区间的点之间的
最短路会在此时正式形成
所以外层的循环random_shuffle⼀下也不会影响正确性
⽆向图最小环
⼀个环可以拆成⼀条最短路加上两条相邻的边的形式
因此可以在用当前点k去更新最短路之前先把i->k k->j两条
边当作环上的两条边去更新最小环
记录pre[i][j] 表示i到j最短路上的第⼀个点
最小环上的点⽆论以什么顺序考虑进来,在考虑到还差⼀
个点k的时候(假设环上与k相邻的点为a,b),其他的点
肯定⽆法更新ab之间的最短路了,不然就会存在更小环
bellman-ford/spfa
⼀个节点的最短距离值最多被更新n-1次,所以
每⼀轮都枚举所有边去更新最短路dis[i]+w[i][j]
-> dis[j],n-1轮之后所有的点的最短路都能更新完
毕,如果第n轮还能继续更新,说明存在负环。
spfa是bellman-ford的队列优化,每次将刚刚被
更新的点放进队列,优先去更新别⼈,知道队
列中元素为空为⽌。
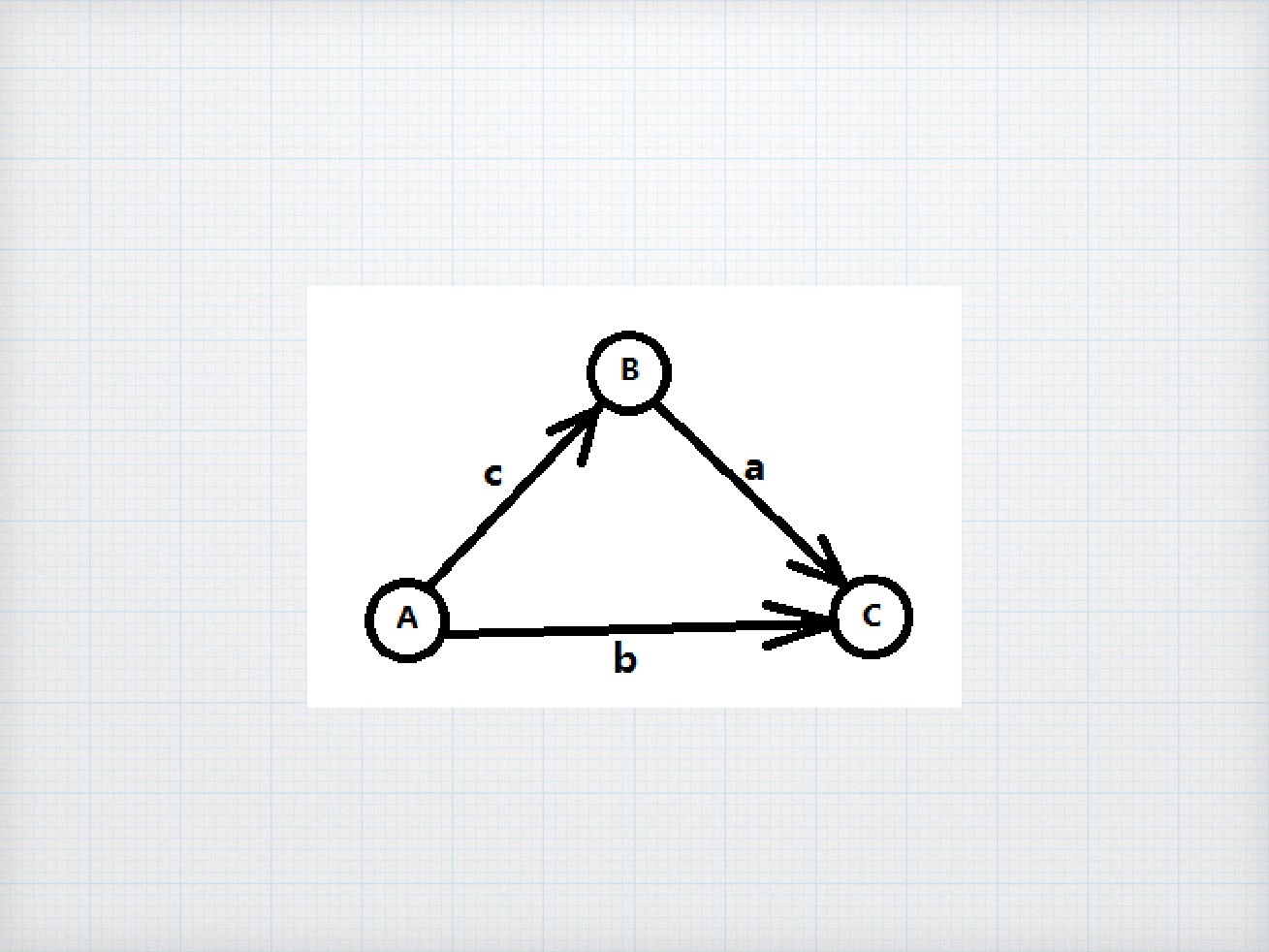
差分约束
B-A<=c
C-B<=a
C-A<=b
求C-A的最⼤值
答案为 min(a+c, b)
拓扑排序
不断的从⼊度为零的点开始bfs,搜到
的点的度数减1,如果bfs结束后有的
点度数不为0,说明有环
字典序最小的最短路
建好最短路图之后直接从起点开始选
择编号小的
图的绝对中⼼
这个中⼼点可以存在与某⼀条边上,
这个点到所有点的最短距离的最⼤值
最小
绝对中⼼到所有点的最短距离的最⼤
值肯定会有两个,⽽且这两个最短距
离位于某条边的两端
反证法
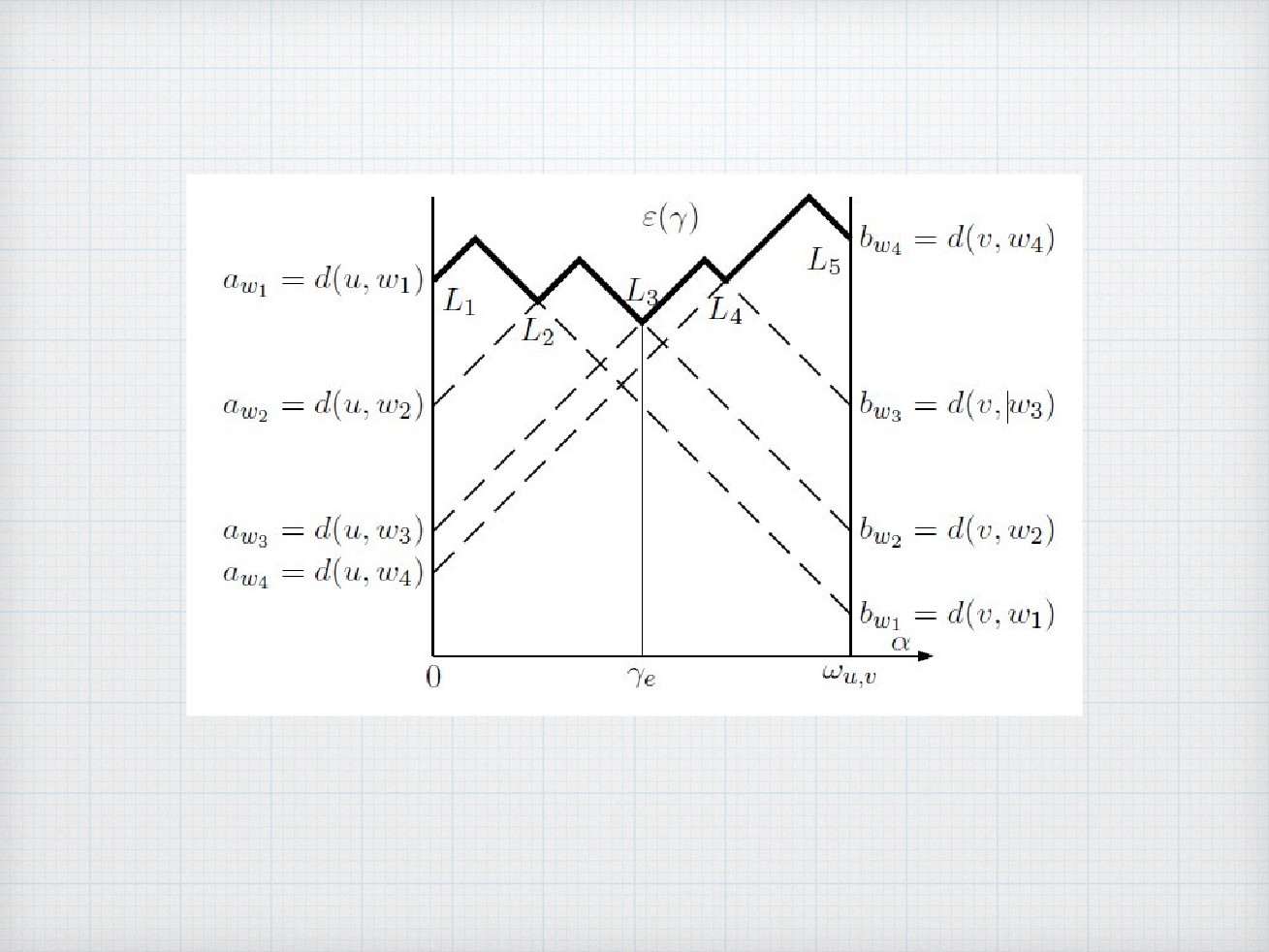
枚举每⼀条边u-v,假设中⼼在这条边
上,那么中⼼到某个点s的距离可以表
示为min(d[u][s] + x, d[v][s]+L-x),数形结
合⼀下发现这个是⼀条折线,每⼀条
边的折线取max构成了⼀个总的折
线,折线的最低点就是答案
最短路径树
每个点记录⼀个最短路径所在的前驱
节点,形成的⼀棵树
最小直径⽣成树MDST
求⼀棵⽣成树,树上最远的两个点距离最
小
先求好绝对中⼼(所在的边上的两个端点u-
v),然后从绝对中⼼出发,位了保证这条
边⼀定在⽣成树上,⼀开始应该设设d[u],
d[v]为真实的值(double),然后搜出⼀颗
最短路径树就是答案